learning_notes

学习笔记

View project on GitHub

优化器

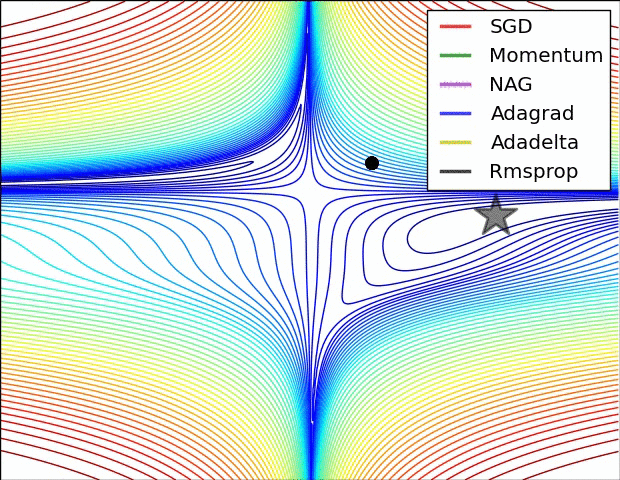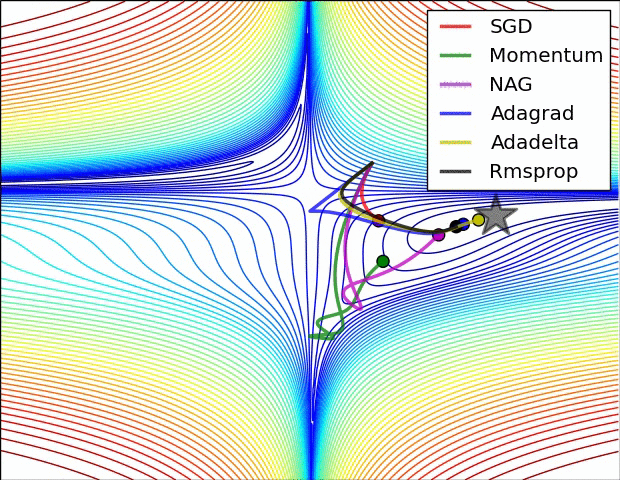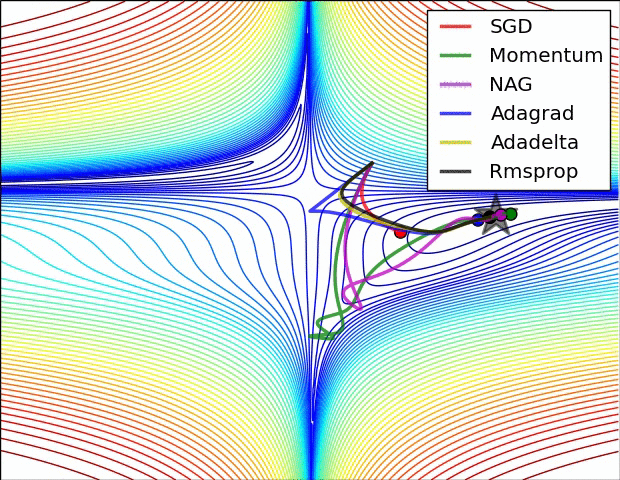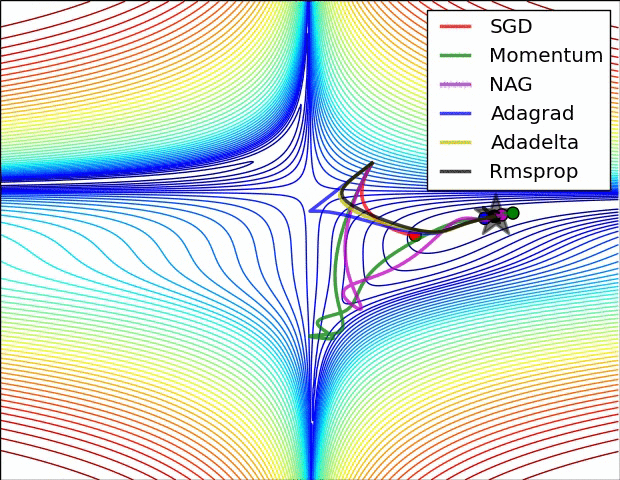
使用动量且改变学习率，会使得收敛加速且减少波动 学习速率

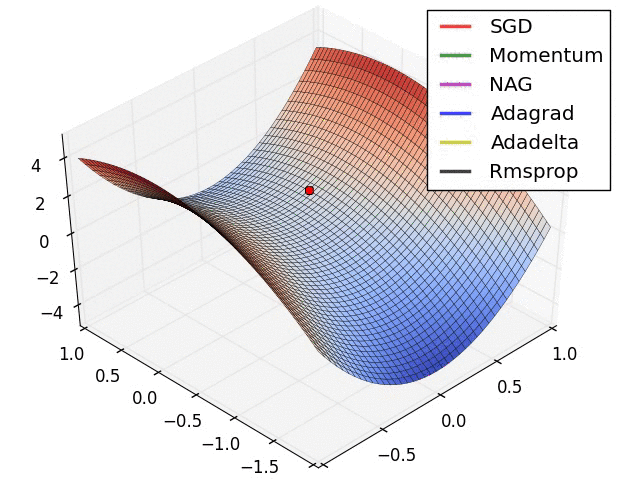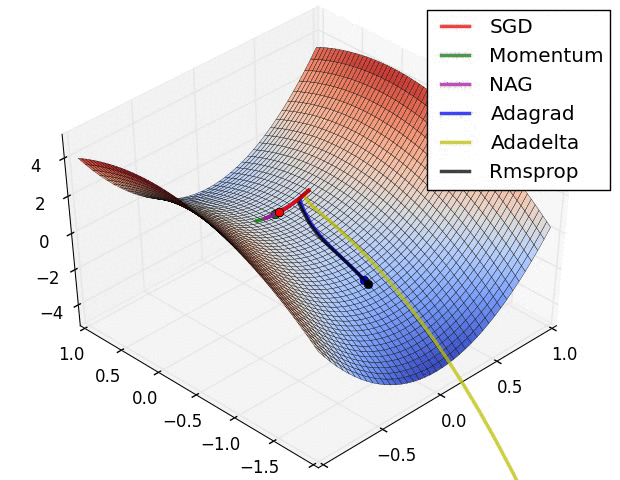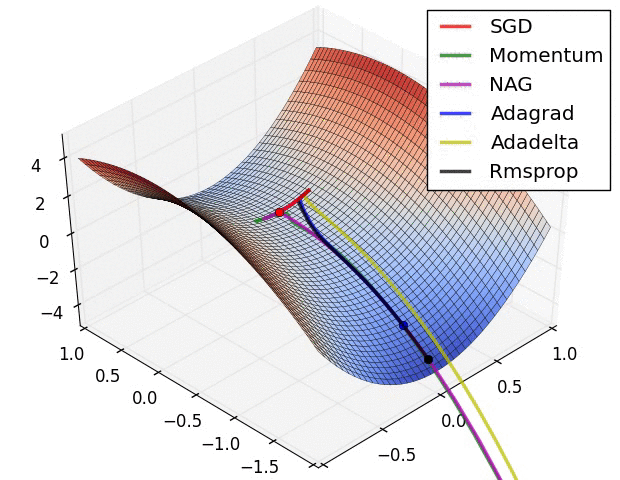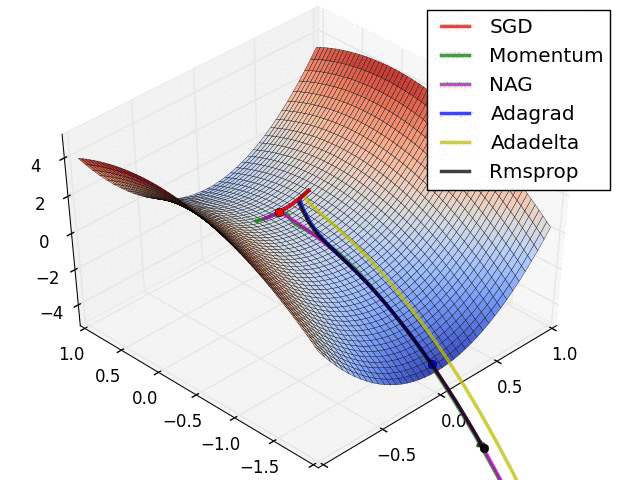
分类

  • 学习率固定
    • BGD
    • SGD
    • MBGD
    • momentum SGD
    • Nesterov SGD 牛顿动量
  • 学习率自适应

优化器介绍

  • BGD 批量梯度下降(Batch Gradient Descent)
    • 缺点:收敛速度慢，大量重复计算
    • 优点:凸函数可以收敛到全局极小值,非突函数收敛到局部极小值 ```bash

      参数

      learning_rate:学习速率 ,决定步子多大 epoch:迭代次数 Momentum: 更新规则 一般0.9

```

  • SGD 随机梯度下降(Stochastic Gradient Descent)
    • 缺点:噪音大,每次不是向最优方向,非全局最优
    • 优点:数据量小,快

  • momentum SGD 动量 更新当前参数时既考虑当前梯度，又考虑之前的梯度（称之为动量）

  • Nesterov SGD 牛顿动量 牛顿法在选择方向时，不仅会考虑坡度是否够大，还会考虑你走了一步之后，坡度是否会变得更大。所以，可以说牛顿法比梯度下降法看得更远一点，能更快地走到最底部 牛顿法添加了校正因子,添加了校正因子的momentum, 即先用旧的动量更新一遍参数，然后再依据momentum的流程走

  • MBGD 微型批量梯度下降(Mini-Batch Gradient Descent)

  • AdaGrad:
    • 根据参数出现的频率调整,频率高–>更新小
  • RMSProp:
    • 改进梯度累积为指数衰减的移动平均，对非凸函数友好
    • 其实RMSprop依然依赖于全局学习率
    • 适合处理非平稳目标 - 对于RNN效果很好
    • RMSprop算是Adagrad的一种发展，和Adadelta的变体，效果趋于二者之间
  • Adam SGD (Momentum + RMSProp):
    • 结合了momentum和RMSProp，同时也引入了修正项（即衰减的指数梯度累积，和衰减的动量累积）
    • 过偏置校正后，每一次迭代学习率都有个确定范围，使得参数比较平稳

  • AdaBound adam + sdg

  • Adadelta: Adadelta是对Adagrad的扩展，最初方案依然是对学习率进行自适应约束，但是进行了计算上的简化。 Adagrad会累加之前所有的梯度平方，而Adadelta只累加固定大小的项，并且也不直接存储这些项，仅仅是近似计算对应的平均值

  • Nadam:
    • Nadam类似于带有Nesterov动量项的Adam
    • Nadam对学习率有了更强的约束

如何优化算法

  • 如果数据是稀疏的,就用自适应方法,即 Adagrad, Adadelta, RMSprop, Adam
  • RMSprop, Adadelta, Adam 在很多情况下的效果是相似的
  • Adam 就是在 RMSprop 的基础上加了 bias-correction 和 momentum
  • 随着梯度变的稀疏，Adam 比 RMSprop 效果会好
  • 一般 Adam 是最好的选择
  • SGD 虽然能达到极小值，但是比其它算法用的时间长，而且可能会被困在鞍点
  • 如果需要更快的收敛，或者是训练更深更复杂的神经网络，需要用一种自适应的算法

其他解释

  • Momentum: momentum是模拟物理里动量的概念，积累之前的动量来替代真正的梯度 加速SGD，抑制振荡，从而加快收敛

  • Nesterov: nesterov项在梯度更新时做一个校正，避免前进太快，同时提高灵敏度

  • 牛顿法：

从本质上去看，牛顿法是二阶收敛，梯度下降是一阶收敛，所以牛顿法就更快。如果更通俗地说的话，比如你想找一条最短的路径走到一个盆地的最底部，梯度下降法每次只从你当前所处位置选一个坡度最大的方向走一步，牛顿法在选择方向时，不仅会考虑坡度是否够大，还会考虑你走了一步之后，坡度是否会变得更大。所以，可以说牛顿法比梯度下降法看得更远一点，能更快地走到最底部。（牛顿法目光更加长远，所以少走弯路；相对而言，梯度下降法只考虑了局部的最优，没有全局思想。）

根据wiki上的解释，从几何上说，牛顿法就是用一个二次曲面去拟合你当前所处位置的局部曲面，而梯度下降法是用一个平面去拟合当前的局部曲面，通常情况下，二次曲面的拟合会比平面更好，所以牛顿法选择的下降路径会更符合真实的最优下降路径。

优点：二阶收敛，收敛速度快；

缺点：牛顿法是一种迭代算法，每一步都需要求解目标函数的Hessian矩阵的逆矩阵，计算比较复杂。

  • 拟牛顿法：

拟牛顿法的本质思想是改善牛顿法每次需要求解复杂的Hessian矩阵的逆矩阵的缺陷，它使用正定矩阵来近似Hessian矩阵的逆，从而简化了运算的复杂度。

  • 共轭梯度法：

共轭梯度法是介于最速下降法与牛顿法之间的一个方法，它仅需利用一阶导数信息，但克服了最速下降法收敛慢的缺点，又避免了牛顿法需要存储和计算Hesse矩阵并求逆的缺点，共轭梯度法不仅是解决大型线性方程组最有用的方法之一，也是解大型非线性最优化最有效的算法之一。